زاوية
الزاوية ولّا لقنيتة ف لهندسة دلماط (ب نّݣليزية: Angle) هي واحد شكل تسطاري، كينتج على لملاقية ديال جوج شعاعات ف نقطة[1]، و كيتسماو هاد الشعاعات ضلوع ديال الزاوية، و النقطة لي كيتلاقاو فيها كتسما راس د زاوية.
عرّف لعالم ليوناني إقليدس الزاوية ف المستوى بلي هي لميل ديال شي مستقيم واحد على واحد أخور، بحيت يكونو هاد زوج مستقيمات كيتلاقاو ف نقطة و ميكونوش متوازيين.[2]


على قبل لعبار ديال شي زاوية θ، كنرسمو قوس كيتمركز ف الراس د الزاوية ب لواسطة ديال لبركار. و كنشدو طول د لقوس s وكنقسموه على نص القطر r و كنضربوه ف لعامل ديال التكبير k. و كنعتمدو على لعبرة لي عندنا، و هادشي كيعطينا هاد لعلاقة:
باش نعبرو شي زاوية، كنعبرو طول د لقوس ديال الدوايرة لي لمركز ديالها هو نقطة ديال تقاطع ديال جوج ضلوع ديالها لي محصور بين جوج ضلوع ديال الزاوية، و كنقسمو هادشي على لمحيط ديال دوايرة. هداك الناتج إيلا ضربناه فنسبة 2 كيكون لقياس ديال زاوية ب لقياس الدائري. و إيلا بغينا نحسبو لقياس ديال زاوية ب الدرجات، كنضربو هداك الناتج ف نمرة 360. و كنعتو على درجة برمز ديال دوايرة صغيورة كترسم فلفوق ديال لقياس د زاوية كيما ف 360°.[3]
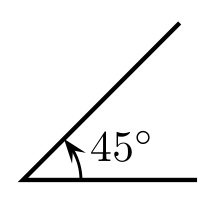
- الدرجة، و هي 1/360 من الزاوية ديال شي دوايرة كاملة.
- الدقيقة، و كتعادل 1/60 من الدرجة.
- الثانية، و كتعادل 1/60 من الدقيقة.
- الراديان، بحيت كيتعتابر لقياس ديال زاوية د شي دوايرة كاملة 2π راديان. ومنو، فراه 1 راديان كيعادل 57.2958 درجة.
- زاوية واقفة، وهي كتعادل 90 درجة ولا π/2 راديان.[4]

|

|

|

|

|

|
| زاوية خاوية | زاوية حادَّة | زاوية واقفة | زاوية واسعة | زاوية مسڭدة | زاوية منعاكسة |
 |
 |
- زاوية واقفة: إيلا قسمنا الزاوية لمسڭدة 180 على زوج د لأقسام متساويين، فراه كول قسم منهم غيولي زاوية واقفة، و لعبار ديالها غيكون 90 درجة.
- زاوية حادة: هي الزاوية لي عبارها قل من 90 درجة.
- زاوية واسعة: هي الزاوية لي عبارها كبر من 90 درجة وصغر من 180 درجة.
- زاوية مسڭدة: هي زاوية لي ضلوعا بزوج ديالها، مقادين بزوج تقادة وحدة، و ف زوج تجاهات مختالفة 180 درجة.
- زاوية منعادمة: هي الزاوية لي عبارها 0 درجة.
- جوج زاويات متساويين: هوما زوج د زاويات عندهم عبار متساوي.
- زاويات كيتشاركو ب راس: هوما زوج زاويات كيتشاركو فنفس الراس و الضلوع.
- زاويات متتامين: هوما زوج زاويات لي لمجموع د عبارهم هو 90 درجة.
- زاويات متكاملين: هوما زوج زاويات لي لمجموع د عبارهم 180 درجة.
- جوج زاويات متجاورتين: هوما زوج زاويات كيتشاركو فنفس الضلع.
- الزاويات لمتبادلين ب الراس: وهي عبارة على زوج د زاويات كيتشكلو إيلا كان شي زوج مستقيمات متوازيين و عندهم شي قاطع (ماشي معامد)، دكشي باش كنقولو بلي جميع زاويات لي كتواجد فالداخل هي زاويات داخلية. أما لي على برا فهي زاويات برانية. و كنقولو على شي زاويات بلي هما متبادلين داخليا و برانيا فاش كيكونو متقابلين و متقايسين. أما الزاويات لمتناظرات (لمتماثلات) فهما الزاويات لي واقعين على نفس جهة من لقاطع، و وحدة فيهم كتكون مابين زوج مستقيمات لمتوازيين (لداخل) و لوخرة على برا. و كنلقاو الزاويات لمتكاملات فاش كنجمعو زوج زاويات دخلانيين، كاينين على نفس الجهة د لقاطع. و كنلقاو 180 درجة.
- ^ Sidorov 2001
- ^ Slocum 2007
- ^ Mathwords: Reference Angle مؤرشف 2018-09-28 فموقع وايباك ماشين
- ^ Wong & Wong 2009







